Auf den ersten Blick scheint Geschichte mit Mathematik für viele Schüler*innen nur wenig gemeinsam zu haben. Dabei ist ja klar, dass die Mathematik auch eine Geschichte hat und viele mathematische Sätze und Erkenntnisse sich irgendwann z.B. aus praktischen Überlegungen heraus ergeben haben. Der Mathematik Leistungskurs der Jahrgangsstufe Q1 betrachtete ein für Schüler*innen heute sehr bedeutsames mathematisches Thema aus historischer Perspektive. Gemeinsam mit der Dozentin für Didaktik und Geschichte der Mathematik Dr. Susanne Spies der Universität Siegen erarbeiteten die Schüler*innen die historische Genese der Differentialrechnung.
Corona zum Trotz entdeckten sie unter Einbindung von Videos, Podcasts und original Vorlesungstexten von Johann Bernoulli aus dem Jahre 1661 eine rein geometrische Herangehensweise an das Tangentenproblem. Ganz ohne Funktionsterm und Koordinatensystem, nur aus der geometrischen Fragestellung nach der Konstruktion einer Tangente an eine „Kurve“ heraus hat Johann Bernoulli einen Zugang zur Differenzialrechnung gefunden, der sich mit den Ergebnissen der heute üblichen Herangehensweise an Schulen an die Differentialrechnung deckt. Die Schüler*innen konnten so einen Blick auf die Ursprünge eines der bedeutendsten Themengebiete der Mathematik erlangen und auch beobachten, wie schon vor fast 400 Jahren Wissenschaftler auch über lange Distanzen hinweg wissenschaftliche Streitgespräche und Diskussionen führten und so die Wissenschaft vorantrieben.
In einem fiktiven Abschlussbrief von Marquise de l´Hospital an seinen Kollegen Johann Bernoulli brachten die Schüler*innen ihre Fragen und Erstaunen über die kennengelernten Methoden und Vorgehensweisen zum Ausdruck: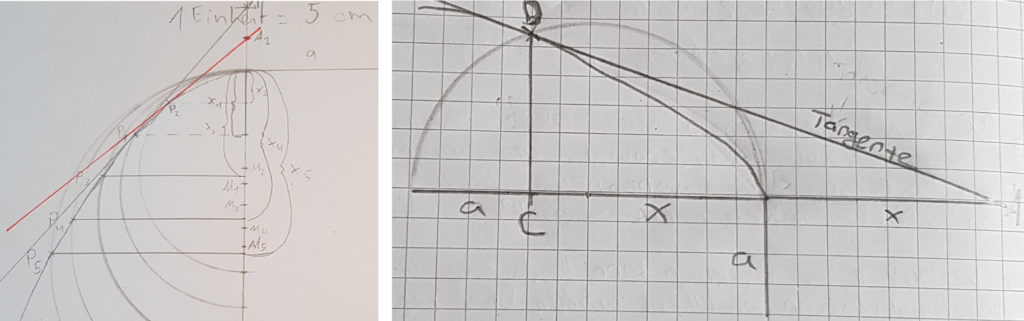 
„Ich finde es spannend zu sehen, dass diese Möglichkeit der Konstruktion einer Tangente an eine Parabel mit Hilfe des Strahlensatzes funktioniert. (…) Funktioniert diese Methode auch für andere Funktionen, z.B. auch für Funktionen, die wir noch nicht kennen? Wie sieht es aus mit Funktionen, die die x-Achse nie berühren?“
„Es wundert mich, dass diese Art der Differentialrechnung an Schulen rein gar nicht vertreten ist – oder regulär gelehrt wird und frage mich, welchen Grund dies haben könnte, wo es doch unzweifelhaft zu einem tieferen Verständnis der Mathematik beitragen könnte.“
„Ist es möglich auf diese (geometrische) Weise auch Extrempunkte oder Wendepunkte zu konstruieren?“
R. Junker